FFT approximation. (Not yet written) See Katoh et al. (2002).
k-mer counting. To accelerate the initial calculation of the distance matrix, which requires a CPU time of O(N2) steps, a rough method similar to the 'quicktree' option of ClustalW is adopted, in which the number of k-mers shared by a pair of sequences is counted and regarded as an approximation of the degree of similarity. MAFFT uses the very rapid method proposed by Jones et al. (1992) with a minor modification (Katoh et al. 2002): (1) The 20 amino acids are compressed to 6 alphabets, according to Dayhoff et al. (1978), and (2) MAFFT performs the second progressive alignment (FFT-NS-2) in order to improve the accuracy.
Modified UPGMA. A modified version of UPGMA is used to construct a guide tree, which works well for handling fragment sequences.
The second progressive alignment. The accuracy of the second progressive alignment (FFT-NS-2) is slightly higher than that of the first progressive alignment (FFT-NS-1) according to the BAliBASE test, but the amount CPU time required by FFT-NS-2 is approximately two times longer than that by FFT-NS-1.
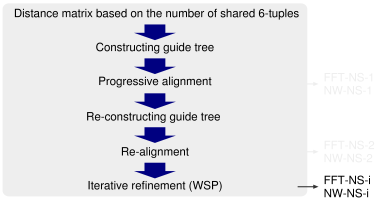
Objective function. The weighted sum-of-pairs (WSP) score proposed by Gotoh is used.
Tree-dependent partitioning. (Not yet written) See Hirosawa et al.
Effect of FFT. To test the effect of the FFT approximation, we also implemented the NW-NS-x options, in which the FFT approximation is disabled, but the other procedures are the same as those in the corresponding FFT-NS-x. There was no significant reduction in the accuracy by introducing the FFT approximation (Katoh et al. 2002).
For pairwise alignment, three different types of algorithms are implemented, global alignment (Needleman-Wunsch), local alignment (Smith-Waterman) with affine gap costs (Gotoh) and local alignment with generalized affine gap costs (Altschul). The differences in the accuracy values among these methods are small for the currently available benchmarks, as shown here. However, each of them has different characteristics, according to the algorithm in the pairwise alignment stage:
oooooooooXXX------XXXXooooooooooo---------------oooooooXXXXXooooooooooooooooo--oooooooooooooooo ---------XXXXX----XXXXoooooooooooooooooooooooooooooooooXXXXX-ooooooooooooooooooooooo----------- oooooooo-XXXXX----XXXX---------------------------------XXXXX---oooooooooo--oooooooooooo-------- ---------XXXXXX---XXXX---------------------------------XXXXX----------------------------------- ---------XXXXXXXXXXXXX---------------------------------XXXXX----------------------------------- ---------XX-------XXXX---------------------------------XXXXX-----------------------------------where 'X's indicate alignable residues, 'o's indicate unalignable residues and '-'s indicate gaps. Unalignable residues are left unaligned at the pairwise alignment stage, because of the use of the generalized affine gap cost. Therefore E-INS-i is applicable to a difficult problem such as RNA polymerase, which has several conserved motifs embedded in long unalignable regions. As E-INS-i has the minimum assumption of the three methods, this is recommended if the nature of sequences to be aligned is not clear. Note that E-INS-i assumes that the arrangement of the conserved motifs is shared by all sequences.
Updated! (2015/Jun) Parameters for E-INS-i have been changed in version 7.243. The new parameters work better for aligning a set of long sequences and short sequences that are closely related to each other. To disable this change, add the --oldgenafpair option.
With the new parameters, E-INS-i may be able to align multiple cDNAs and multiple genomic sequences of a gene from closely related species. However, it consumes large memory space when the sequences are long.
L-INS-i
mafft --localpair --maxiterate 1000 input_file > output_file
or
linsi input_file > output_file
is suitable to:
ooooooooooooooooooooooooooooooooXXXXXXXXXXX-XXXXXXXXXXXXXXX------------------ --------------------------------XX-XXXXXXXXXXXXXXX-XXXXXXXXooooooooooo------- ------------------ooooooooooooooXXXXX----XXXXXXXX---XXXXXXXooooooooooo------- --------ooooooooooooooooooooooooXXXXX-XXXXXXXXXX----XXXXXXXoooooooooooooooooo --------------------------------XXXXXXXXXXXXXXXX----XXXXXXX------------------L-INS-i can align a set of sequences containing sequences flanking around one alignable domain. Flanking sequences are ignored in the pairwise alignment by the Smith-Waterman algorithm. Note that the input sequences are assumed to have only one alignable domain. In benchmark tests, the ref4 of BAliBASE corresponds to this. The other categories of BAliBASE also correspond to similar situations, because they have flanking sequences. L-INS-i also shows higher accuracy values for a part of SABmark and HOMSTRAD than G-INS-i, but we have not identified the reason for this.
G-INS-i
mafft --globalpair --maxiterate 1000 input_file > output_file
or
ginsi input_file > output_file
is suitable to:
XXXXXXXXXXX-XXXXXXXXXXXXXXX XX-XXXXXXXXXXXXXXX-XXXXXXXX XXXXX----XXXXXXXX---XXXXXXX XXXXX-XXXXXXXXXX----XXXXXXX XXXXXXXXXXXXXXXX----XXXXXXXG-INS-i assumes that entire region can be aligned and tries to align them globally using the Needleman-Wunsch algorithm; that is, a set of sequences of one domain must be extracted by truncating flanking sequences. In benchmark tests, SABmark and HOMSTRAD correspond to this.
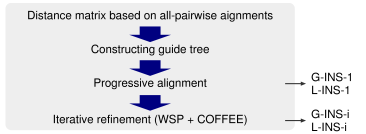
Consistency score. The COFFEE objective function was originally proposed by Notredame et al. (1998), and the extended versions are used in TCoffee and ProbCons. MAFFT also adopts a similar objective function, as described in Katoh et al. (2005). However, the consistency among three sequences (called 'library extension' in TCoffee) is currently not calculated in MAFFT, because the improvement in accuracy by library extension was limited to alignments consisting of a small number (<10) of sequences in our preliminary tests. If library extention is needed, then please use TCoffee or ProbCons.
Consistency + WSP. Instead, the WSP score is summed with the consistency score in the objective function of MAFFT. The use of the WSP score has the merit that a pattern of gaps can be incorporated into the objective function. This is probably the reason why MAFFT achieves higher accuracy than ProbCons and TCoffee for alignments consisting of many (∼10 - ∼100) sequences. This suggests that the pattern of gaps within a group to be aligned is important information when aligning two groups of proteins (and evaluating homology between distantly related protein families).
Scoring matrix for amino acid alignment. The BLOSUM62 matrix is adopted as a default scoring matrix, because this showed slightly higher accuracy values than the BLOSUM80, 45, JTT200PAM, 100PAM and Gonnet matrices in SABmark tests.
Scoring matrix for nucleotide alignment. The default scoring matrix is derived from Kimura's two-parameter model. The ratio of transitions to transversions is set at 2 by default. Other parameters can be used, but have not yet been tested.
Gap penalties for proteins. The default gap penalties for amino acid alignments have been changed in v.4.0. Note that the current version of MAFFT returns an entirely different alignment from v.<4.0. In v.4.0, two major gap penalties (--op [gap open penalty] and --ep [offset value, which functions like a gap extension penalty, see the mafft3 paper for definition]) were tuned by applying the FFT-NS-2 option to a part of the SABmark benchmark. We adopted the parameter set (--op 1.53 --ep 0.123) optimized for SABmark, because this works better for other benchmark (HOMSTRAD, PREFAB and BAliBASE) tests than the previous one (--op 2.4 --ep 0.06). Other parameters might work better in other situations. Consistency-based options have more parameters (L-INS-i has four more parameters and E-INS-i has six more parameters, as explained here). We determined these additional parameters so that the Smith-Waterman alignment function used in L-INS-i returns a local alignment similar to that generated by FASTA, but we have not closely tuned them yet. In our tests using SABmark, the accuracy values can be improved by 2-3% by tuning these parameters, but this improvement may result from overfitting.
Gap penalties for RNAs. The default gap penalties for nucleotide alignment have changed in v.5.6. Note that the current version of MAFFT returns an entirely different alignment from v.<5.6. In the former versions (v.<5.6), the default gap penalties for nucleotide alignments were set at the same values as those for amino acid alignments. According to BRAliBASE, these penalties result in very bad alignments for RNAs. The newer versions (v.≥5.6) use a different penalties for nucleotide alignment; the penalty values are set to three times larger than those for amino acids. This is not yet the optimal value for BRAliBASE. The BRAliBASE score can be improved by closely tuning the penalty values, but we have not adopted the optimized penalties, because we are not sure whether they are applicable to a wide range of problems.
Average score or log expectation score. A different parameter set from from that described above is used in MUSCLE, which has an algorithm similar to that of NW-NS-i. MUSCLE improved in the accuracy of multiple sequence alignment by introducing better parameters than those of the previous version (v3.89) of MAFFT (shown in gray letters in these tables). The latest version of MAFFT uses the re-adjusted gap penalties (see above) with a conventional average score. As Wallace et al. (2005) reported that the log expectation score outperforms the conventional average score, we are planning to examine the effectiveness of the log expectation score proposed in MUSCLE.
The accuracy of an alignment of a few distantly related sequences is considerably improved when they are aligned together with their close homologs. The reason for the improvement is probably the same as that for PSI-BLAST. That is, the positions of highly conserved residues, those with many gaps and other additional information are provided by close homologs. According to Katoh et al. (2005), the improvement by adding close homologs is 10% or so, which is comparable to the improvement achieved by incorporating the structural information of a pair of sequences. Mafft-homologs in the mafft server works like this:
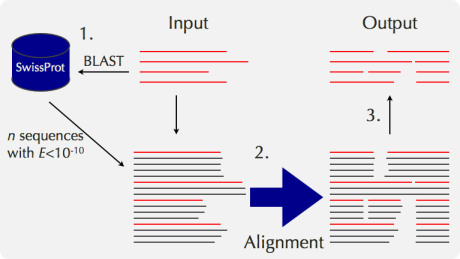
A service based on a similar idea is also available in PRALINE. Note that mafft-homologs aims only to improve the alignment accuracy, but not to comprehensively collect the full-length sequences of homologs. Thus, the resulting alignment with homologs by mafft-homologs is not appropriate for evolutionary analyses. For such a purpose, services with complete sequences, such as PipeAlign, are more appropriate.
When the FFT approximation is used in nucleotide alignment, MAFFT v.5.743 and previous versions convert a nucleotide base to a set of four real numbers. For example, the sequence AACGTCT is converted to a set of four arrays: (1,1,0,0,0,0,0), (0,0,1,0,0,1,0), (0,0,0,1,0,0,0) and (0,0,0,0,1,0,1). In v.5.744, this will be replaced with a more efficient method, according to Rockwood et al. (2005). That is, AACGTCT is converted to (i,i,-1,1,-i,1,-i), where i is an imaginary unit.
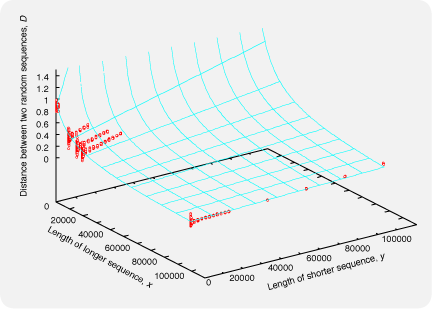
where Sij is the number of shared 6-tuples by sequences i and j. The expected value of Dij between two unrelated sequences depends on the lengths of the sequences; when comparing a very short sequence and a very long sequence, Dij is near 0 by chance, even if the sequences are unrelated to each other. The situation is depicted in the figure below, where the red points indicate Dij calculated for randomly generated aa sequences (by ROSE) with various pairs of lengths. The cyan surface isDij = 1 - Sij / min( Sii, Sjj )
where x and y are the lengths of longer and shorter sequences, respectively. The function f(,) was empirically determined so that the surface is close to the red points. Mafft6 uses Dij' instead of Dij,f(x,y) = y/x * 0.1 + 10000 / ( x + 10000 ) + 0.01
Dij' = Dij / f(x,y).